Ctrl+K

FAC_TMS_2F (dual spacecraft)

FAC_TMS_2F (dual spacecraft)#

Abstract: Access to the field aligned currents evaluated by the dual satellite method (level 2 product). We also show an orbit-by-orbit plot using a periodic axis to display (centred over both poles) an overview of the FAC estimates over two weeks.

See also:

%load_ext watermark
%watermark -i -v -p viresclient,pandas,xarray,matplotlib

Python implementation: CPython
Python version       : 3.11.6
IPython version      : 8.18.0

viresclient: 0.12.0
pandas     : 2.1.3
xarray     : 2023.12.0
matplotlib : 3.8.2

from viresclient import SwarmRequest
import datetime as dt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates

request = SwarmRequest()

FAC_TMS_2F product information#

This is derived from data from both Swarm Alpha and Charlie by the Ampère’s integral method

Documentation:

Check what “FAC” data variables are available#

NB: these are the same as in the FACxTMS_2F single-satellite FAC product

request.available_collections("FAC", details=False)

{'FAC': ['SW_OPER_FACATMS_2F',
  'SW_OPER_FACBTMS_2F',
  'SW_OPER_FACCTMS_2F',
  'SW_OPER_FAC_TMS_2F',
  'SW_FAST_FACATMS_2F',
  'SW_FAST_FACBTMS_2F',
  'SW_FAST_FACCTMS_2F']}

request.available_measurements("FAC")

['IRC',
 'IRC_Error',
 'FAC',
 'FAC_Error',
 'Flags',
 'Flags_F',
 'Flags_B',
 'Flags_q']

Fetch one day#

Also fetch the quasidipole (QD) coordinates at the same time.

request.set_collection("SW_OPER_FAC_TMS_2F")
request.set_products(
    measurements=["FAC", "FAC_Error", 
                  "Flags", "Flags_F", "Flags_B", "Flags_q"],
    auxiliaries=["QDLat", "QDLon"],
)
data = request.get_between(
    dt.datetime(2016,1,1),
    dt.datetime(2016,1,2)
)

data.sources

['SW_OPER_FAC_TMS_2F_20160101T000000_20160101T235959_0401']

Load as a pandas dataframe:

df = data.as_dataframe()
df.head()
Flags Spacecraft QDLat Latitude Flags_B QDLon Longitude Flags_F FAC Radius FAC_Error Flags_q
Timestamp
2016-01-01 00:00:00.500 0 - -81.264999 -72.499886 2002 104.167931 93.510970 22222224 0.044131 6.833866e+06 0.039584 404
2016-01-01 00:00:01.500 0 - -81.299614 -72.563053 2002 103.828697 93.539666 22222224 0.034081 6.833867e+06 0.039720 404
2016-01-01 00:00:02.500 0 - -81.333939 -72.626215 2002 103.486877 93.568594 22222224 0.025312 6.833868e+06 0.039856 404
2016-01-01 00:00:03.500 0 - -81.367966 -72.689371 2002 103.142395 93.597756 22222224 0.019080 6.833870e+06 0.039993 404
2016-01-01 00:00:04.500 0 - -81.401688 -72.752521 2002 102.795349 93.627155 22222224 0.014609 6.833871e+06 0.040132 404

Depending on your application, you should probably do some filtering according to each of the flags. This can be done on the dataframe here, or beforehand on the server using request.set_range_filter(). See https://earth.esa.int/documents/10174/1514862/Swarm-L2-FAC-Dual-Product-Description for more about the data

Load as xarray dataset (we will use this instead of the pandas dataframe)

ds = data.as_xarray()
ds

<xarray.Dataset>
Dimensions:     (Timestamp: 86400)
Coordinates:
  * Timestamp   (Timestamp) datetime64[ns] 2016-01-01T00:00:00.500000 ... 201...
Data variables:
    Spacecraft  (Timestamp) object '-' '-' '-' '-' '-' ... '-' '-' '-' '-' '-'
    Flags       (Timestamp) uint32 0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
    QDLat       (Timestamp) float64 -81.26 -81.3 -81.33 ... 41.33 41.39 41.45
    Latitude    (Timestamp) float64 -72.5 -72.56 -72.63 ... 31.55 31.61 31.68
    Flags_B     (Timestamp) uint32 2002 2002 2002 2002 ... 2002 2002 2002 2002
    QDLon       (Timestamp) float64 104.2 103.8 103.5 ... -24.03 -24.03 -24.03
    FAC_Error   (Timestamp) float64 0.03958 0.03972 0.03986 ... 0.01702 0.01702
    Longitude   (Timestamp) float64 93.51 93.54 93.57 ... -94.65 -94.65 -94.65
    Flags_F     (Timestamp) uint32 22222224 22222224 ... 22222224 22222224
    FAC         (Timestamp) float64 0.04413 0.03408 ... -0.009214 -0.008928
    Radius      (Timestamp) float64 6.834e+06 6.834e+06 ... 6.823e+06 6.823e+06
    Flags_q     (Timestamp) uint32 404 404 404 404 404 404 404 ... 0 0 0 0 0 0 0
Attributes:
    Sources:         ['SW_OPER_FAC_TMS_2F_20160101T000000_20160101T235959_0401']
    MagneticModels:  []
    AppliedFilters:  []

Plot the time series#

ds["FAC"].plot(x="Timestamp");
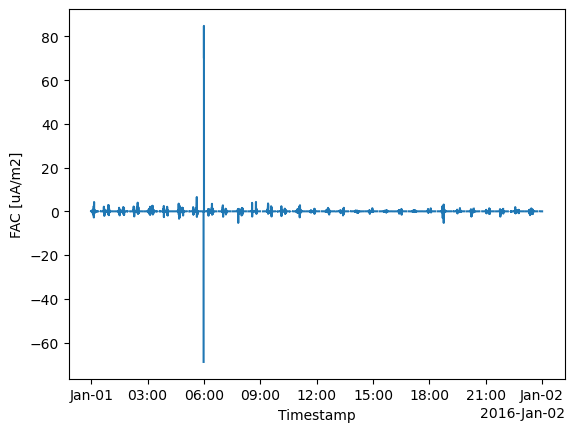
../_images/199eebbeb5ee2ae02adcfec6a60228edffd50f22cd5b79cca9c033d26a76cf65.png 
fig, axes = plt.subplots(ncols=1, nrows=2, figsize=(15,5))
axes[0].plot(ds["Timestamp"], ds["FAC"])
axes[1].plot(ds["Timestamp"], ds["FAC_Error"], color="orange")
axes[0].set_ylabel("FAC\n[$\mu A / m^2$]");
axes[1].set_ylabel("Error\n[$\mu A / m^2$]");
axes[1].set_xlabel("Timestamp");
date_format = mdates.DateFormatter('%Y-%m-%d\n%H:%M')
axes[1].xaxis.set_major_formatter(date_format)
axes[0].set_ylim(-5, 5);
axes[1].set_ylim(0, 1);
axes[0].set_xticklabels([])
axes[0].grid(True)
axes[1].grid(True)
fig.subplots_adjust(hspace=0.1)
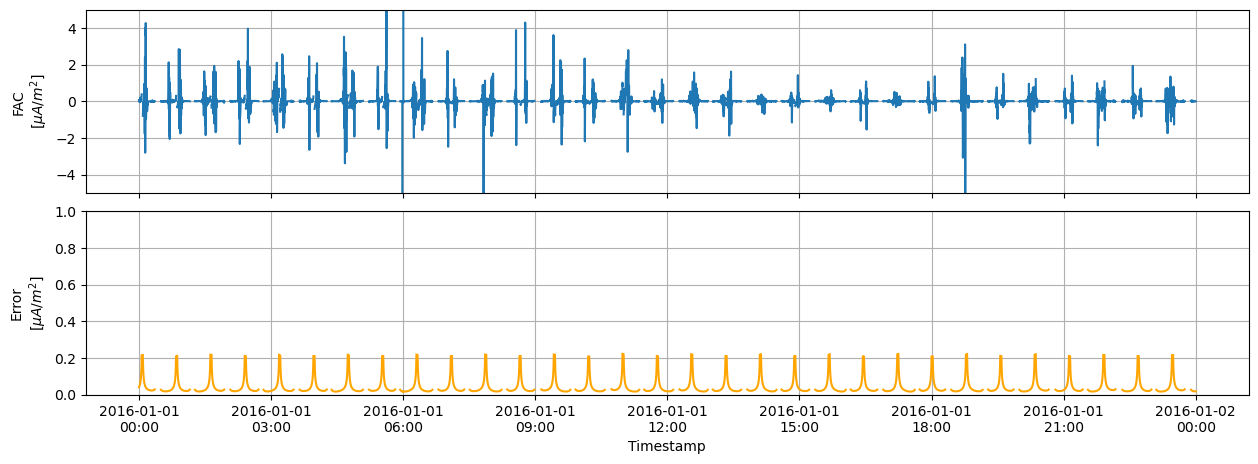
../_images/f2644cb0b5991319a2ecb6eb97ab74d52427aa8095f6482e984e37580611d9f0.png

Note that the errors are lower than with the single satellite product

“2D” plotting of two weeks using periodic axes#

Identify a stormy period between 2016.0 and 2018.0#

# Fetch Dst over this period
# NB this is just a convenient way to fetch Dst in this notebook
#    Not really a good way to do it in general
start_time = dt.datetime(2016,1,1)
end_time = dt.datetime(2018,1,1)
request = SwarmRequest()
request.set_collection("SW_OPER_FAC_TMS_2F")
request.set_products(
    measurements=[],
    auxiliaries=["Dst"],
    sampling_step="PT120M"
)
ds_dst = request.get_between(start_time, end_time).as_xarray()

# Count the occurences of Dst < -50 nT each month
ds_dst["Dst"].where(ds_dst["Dst"]<-50).resample({"Timestamp": "1m"}).count().plot();
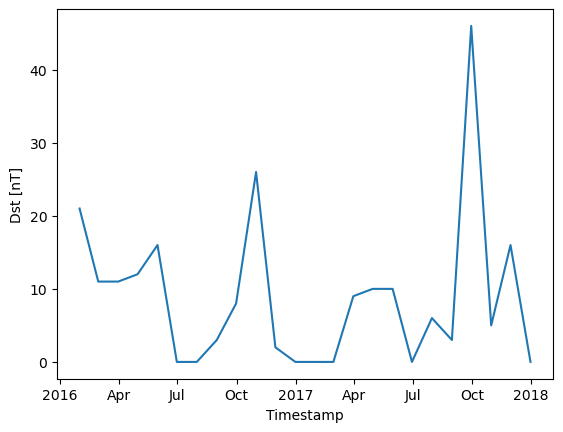
../_images/fe1ad8f05c21f49b813747e2825b0cc21dc2787a6cb05bcb7a7ced5f81b6f76c.png 
# Plot Dst from that peak month to then choose a two-week period from it
ds_dst["Dst"].sel({"Timestamp": slice("2016-10-01","2016-10-30")}).plot();
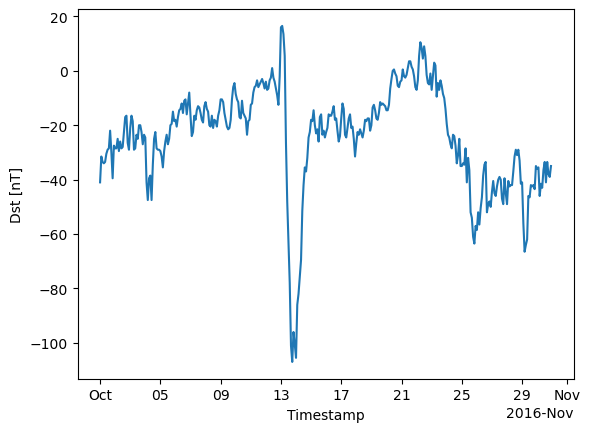
../_images/1c4f25bf15234a0a692e67dcf60b623f5c67d9ab5b2272019c7206d1883da096.png

Fetch the data from the chosen time period#

start_time = dt.datetime(2016,10,9)
## If you want an exact number of days:
end_time = start_time + dt.timedelta(days=14)

request = SwarmRequest()
request.set_collection("SW_OPER_FAC_TMS_2F")
request.set_products(
    measurements=["FAC", "Flags"],
    auxiliaries=["QDLat", "QDLon", "MLT",
                 "OrbitNumber", "QDOrbitDirection"],
    sampling_step="PT10S"
)
data = request.get_between(start_time, end_time)
ds = data.as_xarray()
# NB OrbitNumber is not available for the dual satellite product because it is ambiguous
ds

<xarray.Dataset>
Dimensions:     (Timestamp: 120960)
Coordinates:
  * Timestamp   (Timestamp) datetime64[ns] 2016-10-09T00:00:00.500000 ... 201...
Data variables:
    Spacecraft  (Timestamp) object '-' '-' '-' '-' '-' ... '-' '-' '-' '-' '-'
    Flags       (Timestamp) uint32 104400000 104400000 ... 4400000 4400000
    QDLat       (Timestamp) float64 85.1 84.52 83.94 ... -40.14 -39.54 -38.94
    Latitude    (Timestamp) float64 87.29 87.34 87.23 ... -43.95 -43.31 -42.67
    QDLon       (Timestamp) float64 144.5 143.2 142.1 ... -51.77 -52.08 -52.38
    Longitude   (Timestamp) float64 -36.08 -22.38 -9.023 ... -136.8 -136.7
    MLT         (Timestamp) float64 4.921 4.836 4.767 4.711 ... 15.82 15.8 15.78
    FAC         (Timestamp) float64 nan nan nan ... -0.01751 -0.02754 -0.0245
    Radius      (Timestamp) float64 6.811e+06 6.811e+06 ... 6.829e+06 6.829e+06
Attributes:
    Sources:         ['SW_OPER_FAC_TMS_2F_20161009T000000_20161009T235959_040...
    MagneticModels:  []
    AppliedFilters:  []

Complex plotting setup (experimental)#

# Functions to produce periodic axes
# Source: https://github.com/pacesm/jupyter_notebooks/blob/master/Periodic%20Axis.ipynb
from matplotlib import pyplot as plt
from numpy import mod, arange, floor_divide, asarray, concatenate, empty, array
from itertools import chain
import matplotlib.cm as cm
from matplotlib.colors import Normalize, LogNorm, SymLogNorm
from matplotlib.colorbar import ColorbarBase

class PeriodicAxis(object):
    def __init__(self, period=1.0, offset=0):
        self.period = period
        self.offset = offset

    def _period_index(self, x):
        return floor_divide(x - self.offset, self.period)
    
    def periods(self, offset, size):
        return self.period * arange(self._period_index(offset), self._period_index(offset + size) + 1)
        
    def normalize(self, x):
        return mod(x - self.offset, self.period) + self.offset

# def periodic_plot(pax, x, y, xmin, xmax, *args, **kwargs):
#     xx = pax.normalize(x)
#     for period in pax.periods(xmin, xmax - xmin):
#         plt.plot(xx + period, y, *args, **kwargs)
#     plt.xlim(xmin, xmax)
    
# def periodic_xticks(pax, xmin, xmax, ticks, labels=None):
#     ticks = asarray(ticks)
#     labels = labels or ticks
#     ticks_locations = concatenate([
#         ticks + period
#         for period in pax.periods(xmin, xmax - xmin)
#     ])
#     ticks_labels = list(chain.from_iterable(
#         labels for _ in pax.periods(xmin, xmax - xmin)
#     ))
#     plt.xticks(ticks_locations, ticks_labels)
#     plt.xlim(xmin, xmax)

class PeriodicLatitudeAxis(PeriodicAxis):
    def __init__(self, period=360, offset=-270):
        super().__init__(period, offset)
    
    def periods(self, offset, size):
        return self.period * arange(self._period_index(offset), self._period_index(offset + size) + 1)
        
    def normalize(self, x):
        return mod(x - self.offset, self.period) + self.offset

def periodic_latscatter(pax, x, y, ymin, ymax, *args, **kwargs):
    yy = pax.normalize(y)
    xmin = kwargs.pop("xmin")
    xmax = kwargs.pop("xmax")
    for period in pax.periods(xmin, xmax - xmin):
        plt.scatter(x, yy + period, *args, **kwargs)
    plt.ylim(ymin, ymax)

def periodic_yticks(pax, ymin, ymax, ticks, labels=None):
    ticks = asarray(ticks)
    labels = labels or ticks
    ticks_locations = concatenate([
        ticks + period
        for period in pax.periods(ymin, ymax - ymin)
    ])
    ticks_labels = list(chain.from_iterable(
        labels for _ in pax.periods(ymin, ymax - ymin)
    ))
    plt.yticks(ticks_locations, ticks_labels)
    plt.ylim(ymin, ymax)

def fac_overview_plot(ds):

    fig, axes = plt.subplots(figsize=(16, 8), dpi=100)

    tmp1 = array(ds['QDLat'][1:])
    tmp0 = array(ds['QDLat'][:-1])
    pass_flag = tmp1 - tmp0
    latitudes = tmp0
    times = array(ds['Timestamp'][:-1])
    values = array(ds['FAC'][:-1])

    # # Subsample data
    # pass_flag = pass_flag[::10]
    # latitudes = latitudes[::10]
    # times = times[::10]
    # values = values[::10]

    plotted_latitudes = array(latitudes)
    descending = pass_flag < 0
    plotted_latitudes[descending] = -180 - latitudes[descending]

    vmax = 20
    plax = PeriodicLatitudeAxis()
    periodic_latscatter(
        plax, times, plotted_latitudes, -190, 190, 
        xmin=-360-90, xmax=360+90, c=values, s=1,
        # https://matplotlib.org/tutorials/colors/colormapnorms.html#symmetric-logarithmic
        cmap=cm.coolwarm, norm=SymLogNorm(linthresh=0.1, linscale=1, vmin=-vmax,vmax=vmax)
    )
    cax = plt.colorbar()
    cax.ax.set_ylabel("FAC [$\mu A / m^2$]")
    plt.xlim(times.min(), times.max())
    plt.xlabel("time")
    plt.ylabel("QD-latitude / deg")

    periodic_yticks(plax, -190, +190, [-225, -180, -135, -90, -45,  0, 45,  90], labels=[
        '+45\u2193', '0\u2193', '\u221245\u2193', '\u221290', '\u221245\u2191', '0\u2191', '+45\u2191', '+90'
    ])
    return fig, axes

fac_overview_plot(ds);

/opt/conda/lib/python3.11/site-packages/numpy/ma/core.py:4348: RuntimeWarning: invalid value encountered in subtract
  self._data.__isub__(other_data)
../_images/4eac724868138f8b02c19661aa44f52ebff857d9194e3a10dac3f58b8ee3fad4.png 
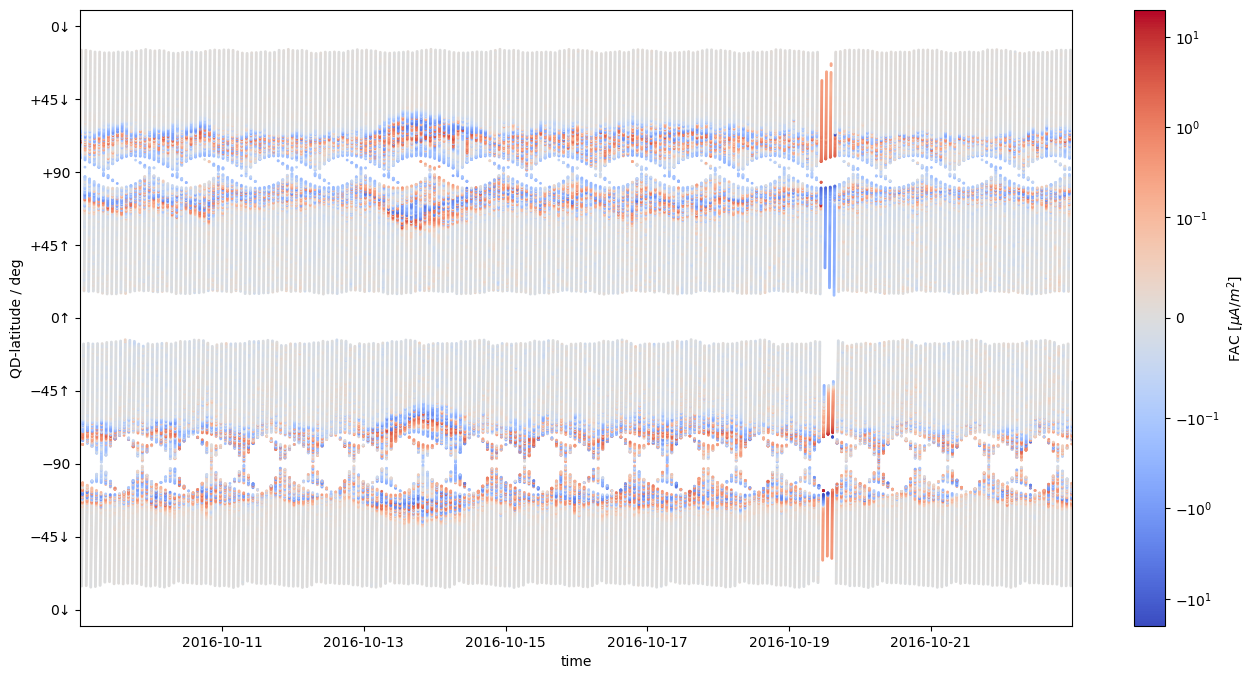
# Maximum values for FAC indicate saturation of the colorbar
ds["FAC"].max(), ds["FAC"].min()

(<xarray.DataArray 'FAC' ()>
 array(65.4033561),
 <xarray.DataArray 'FAC' ()>
 array(-60.04496457))

A few other views of the data#

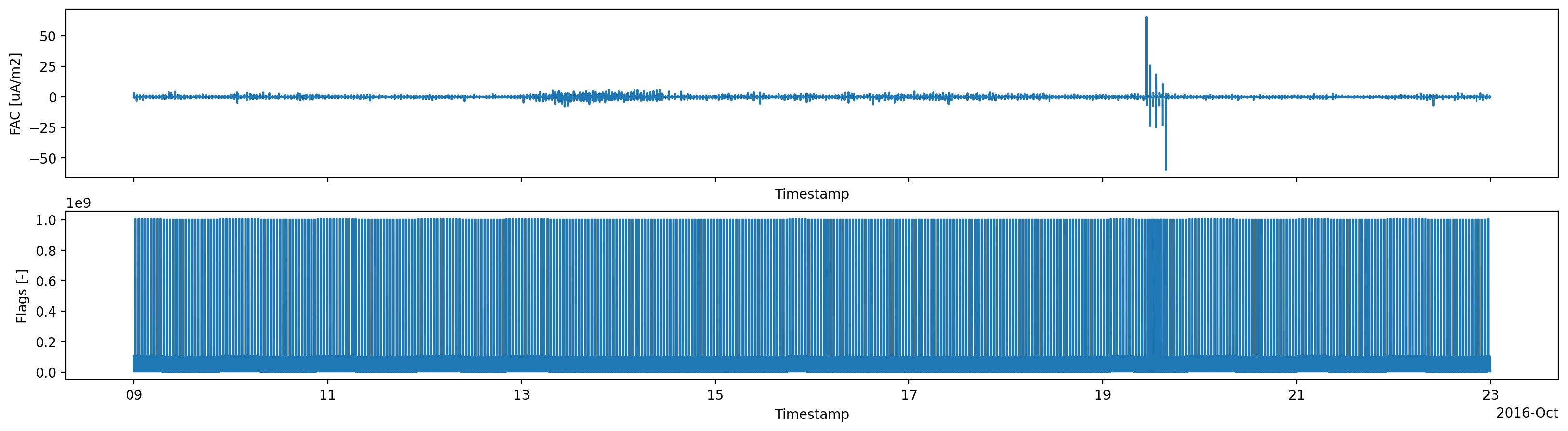
# Flags indicate something wrong around 2016-10-19
fig, axes = plt.subplots(nrows=2, sharex=True, figsize=(20,5), dpi=200)
ds["FAC"].plot(ax=axes[0])
ds["Flags"].plot(ax=axes[1]);
../_images/93153cf91166ad8dec28f0daeae6cd86da82baea425a38260e95bc82377fd0ee.png 
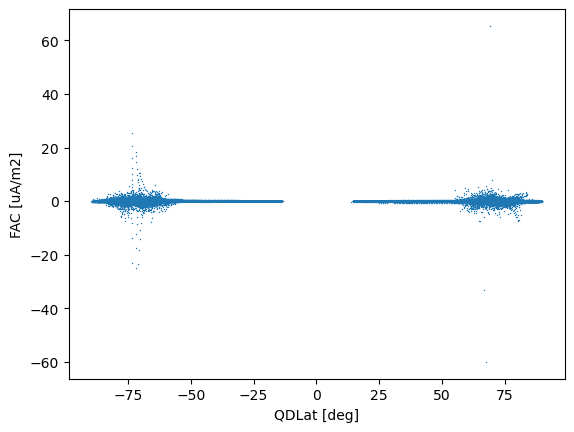
ds.plot.scatter(y="FAC", x="QDLat", s=1, linewidths=0);
../_images/3fdc74ac9c137c4114af0d43dff2f91160ffa608372a6751c11a9d13682b8dd4.png 
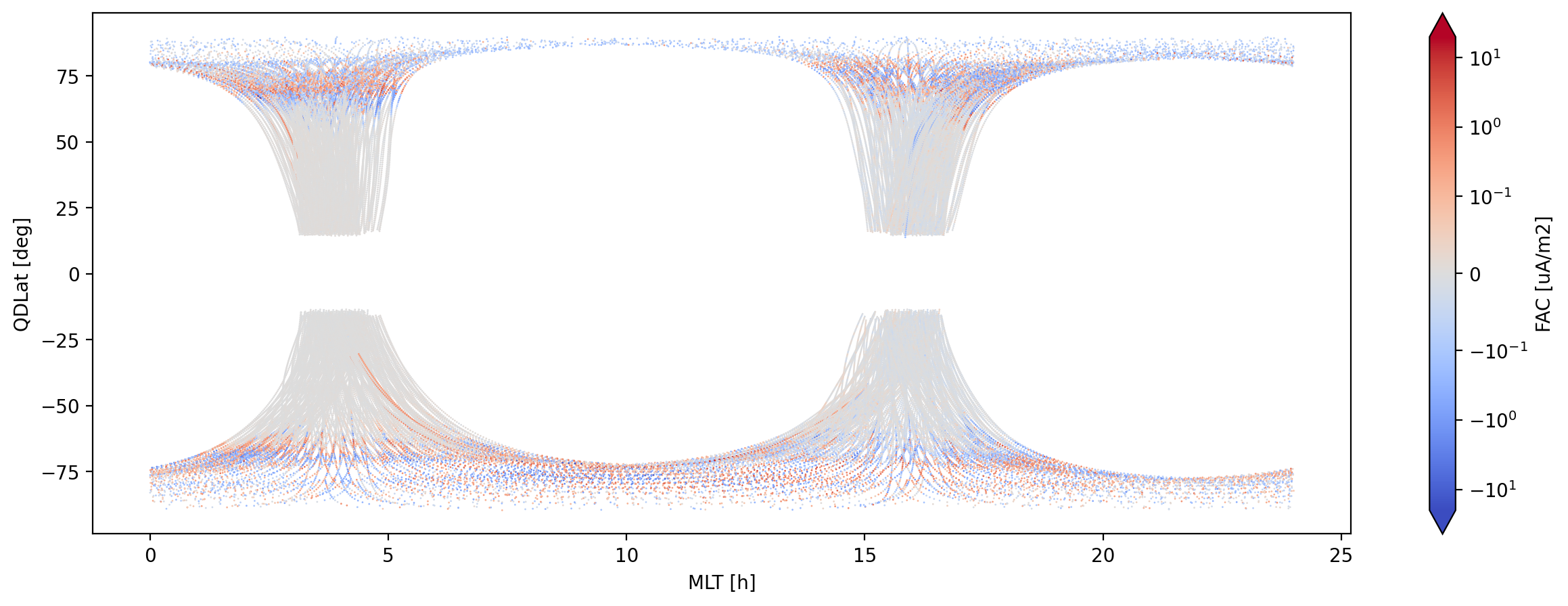
fig, ax = plt.subplots(figsize=(15,5), dpi=200)
ds.plot.scatter(
    ax=ax,
    x="MLT", y="QDLat", hue="FAC", cmap=cm.coolwarm, s=1, linewidths=0,
    norm=SymLogNorm(linthresh=0.1, linscale=1, vmin=-20, vmax=20),
);

/opt/conda/lib/python3.11/site-packages/numpy/ma/core.py:4348: RuntimeWarning: invalid value encountered in subtract
  self._data.__isub__(other_data)
../_images/2114f336f8720565566f196e1a39fea016b5ba680ef79db79469223d6921390d.png 
# Plotting the maximum FAC encountered on each orbit
# Do this with the single satellite product instead for now
#  so that we can quickly use the OrbitNumber parameter
#  which is not available for the dual-sat product
# You could achieve this by generating a flag based on
#  zero-crossings of Latitude
start_time = dt.datetime(2016,10,9)
end_time = start_time + dt.timedelta(days=14)
request = SwarmRequest()
request.set_collection("SW_OPER_FACATMS_2F")
request.set_products(
    measurements=["FAC", "Flags"],
    auxiliaries=["QDLat", "QDLon", "MLT",
                 "OrbitNumber", "QDOrbitDirection"],
    sampling_step="PT10S"
)
data = request.get_between(start_time, end_time)
ds = data.as_xarray()
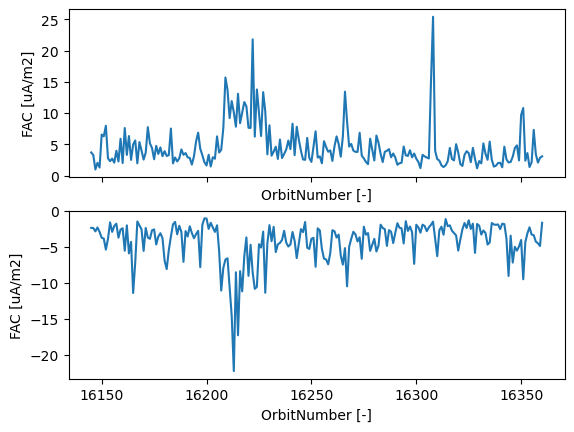
fig, axes = plt.subplots(nrows=2, sharex=True)
ds.groupby("OrbitNumber").max()["FAC"].plot(ax=axes[0])
ds.groupby("OrbitNumber").min()["FAC"].plot(ax=axes[1]);
../_images/d3021277e8dc2dc9bf636247ba98a49f042b3a72f8d603be559b9c01a2fe7c35.png
Contents